APLICACIONES DE LAS DERIVADAS 

El deseo de medir y de cuantificar el cambio, la variación, condujo en el siglo XVII hasta la noción de derivada. 

El estudio de las operaciones con derivadas, junto con las integrales, constituyen el cálculo infinitesimal. Los introductores fueron Newton y Leibnitz, de forma independiente. Los conceptos son difíciles y hasta bien entrado el siglo XIX no se simplificaron. A ello contribuyó la aparición de una buena notación, que es la que usaremos. Las aplicaciones prácticas de esta teoría no dejan de aparecer.

Consideremos la gráfica de abajo  en la que se tiene el recorrido de un ciclista en una carrera; en ella se observan desniveles en el recorrido,  se tiene un primer trozo en el que el ciclista sube,

  después baja y por último sube otra vez hasta llegar a la meta. Pretendemos formalizar el concepto "subir" en la gráfica de una función, para ello tomemos dos puntos x e y del eje X y obtengamos sus asociados del eje Y, se observa que si x<y entonces se tendrá que f(x)<f(y).     Si por el contrario tomamos dos puntos del eje X en los que la función "baja" con x<y y obtenemos sus asociados del eje Y, se tiene que debido a la bajada f(x) tiene que ser mayor que f(y).
 

Definición 1.- Sea un intervalo y sea f una función con dominio I. Entonces:
 

• Decimos que f es creciente en I si  x, y  I,  tales que x<y se tiene que f(x) f(y)
• Decimos que f es decreciente en I si  x, y I tales que x<y se tiene que f(y) f(x)

Si una función es creciente o decreciente diremos que es monótona.

•  Decimos que f es estrictamente creciente en I si  x,y I tales que x<y se tiene que f(x)<f(y)

• Decimos que f es estrictamente decreciente en I si x,y I tales que x<y se tiene que f(y)<f(x)

• Si una función es estrictamente creciente o estrictamente decreciente diremos que es estrictamente monótona.

  

MOVIMIENTO RECTILINEO

Se denomina movimiento rectilíneo, aquél cuya trayectoria es una línea recta.

En la recta situamos un origen O, donde estará un observador que medirá la posición del móvil x en el instante t. Las posiciones serán positivas si el móvil está a la derecha del origen y negativas si está a la izquierda del origen.

Posición

La posición x del móvil se puede relacionar con el tiempo t mediante una función x=f(t).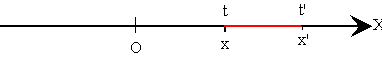

Desplazamiento
Supongamos ahora que en el tiempo t, el móvil se encuentra en posición x, más tarde, en el instante t' el móvil se encontrará en la posición x'. Decimos que móvil se ha desplazado Dx=x'-x en el intervalo de tiempo Dt=t'-t, medido desde el instante t al instante t'.

La velocidad media entre los instantes t y t' está definida por

Para determinar la velocidad en el instante t, debemos hacer el intervalo de tiempo Dt tan pequeño como sea posible, en el límite cuando Dt tiende a cero.

Pero dicho límite, es la definición de derivada de x con respecto del tiempo t.
Para comprender mejor el concepto de velocidad media, resolvemos el siguiente ejercicio

Ejercicio

Una partícula se mueve a lo largo del eje X, de manera que su posición en cualquier instante t está dada por x=5·t²+1, donde x se expresa en metros y t en segundos.

Calcular su velocidad promedio en el intervalo de tiempo entre:

•  2 y 3 s.
•  2 y 2.1 s.
•  2 y 2.01 s.
•  2 y 2.001 s.
•  2 y 2.0001 s.
•  Calcula la velocidad en el instante t=2 s.

En el instante t=2 s, x=21 m
t’ (s)	x’ (m)	Δx=x'-x	Δt=t'-t	m/s
3	46	25	1	25
2.1	23.05	2.05	0.1	20.5
2.01	21.2005	0.2005	0.01	20.05
2.001	21.020005	0.020005	0.001	20.005
2.0001	21.00200005	0.00200005	0.0001	20.0005
...	...	...	...	...
			0	20

Como podemos apreciar en la tabla, cuando el intervalo Δt→0, la velocidad media tiende a 20 m/s. La velocidad en el instante t=2 s es una velocidad media calculada en un intervalo de tiempo que tiende a cero.

Calculamos la velocidad en cualquier instante t

• La posición del móvil en el instante t es x=5t²+1
• La posición del móvil en el instante t+Dt es  x'=5(t+Dt)²+1=5t²+10tDt+5Dt²+1
• El desplazamiento es Dx=x'-x=10tDt+5Dt²
• La velocidad media <v> es

La velocidad en el instante t es el límite de la velocidad media cuando el intervalo de tiempo tiende a cero

La velocidad en un instante t se puede calcular directamente, hallando la derivada de la posición x respecto del tiempo.

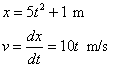
En el instante t=2 s, v=20 m/s

VALORES EXTREMOS DE UNA FUNCIÓN

La función f(x)=x³ - x² - 12x no tiene extremos absolutos en el intervalo abierto (-4,5), ¿por qué? Fíjate en la siguiente gráfica:

f(x)= x3 - x2 -12x f'(x)= 3x2 - 2x -12 Números críticos: {-1.69425, 2.36092}

    Si prestamos atención a los valores de la función para aquellas x's cercanas a (o en la vecindad de) x=c₁ y x=c₂ (los puntos azules de la gráfica), observarás que f(c₁) es el valor máximo de la función en un intervalo (a₁,b₁) que contenga a c₁ y f(c₂) es el valor mínimo de la función en un intervalo (a₂,b₂) que contenga a c₂.

    Estos puntos reciben el nombre de extremos relativos o locales, y se definen como sigue:

 Definición de extremo relativo:

• Un número y₁=f(c₁) es un máximo relativo de una función f, si f(x) f(c₁) para toda x en algún intervalo abierto que contenga a c₁.
• Un número y₁=f(c₁) es un mínimo relativo de una función f, si f(x)f (c₁) para toda x en algún intervalo abierto que contenga a c₁.

  Es importante notar que f(c) debe estar definida para que el número c sea un valor crítico. Enunciamos en seguida dos importantes teoremas.

Teorema:

Si una función f(x) tiene un extremo relativo en un número c, entonces c es un valor crítico.

APLICACIONES EN LA ARQUITECTURA

Un fondo de inversión genera una rentabilidad que depende de la cantidad de dinero invertida, según la formula: R(x)=-0.002x²+0.8x-5 donde R(x) representa la rentabilidad generada cuando se invierte la cantidad x. Determinar, teniendo en cuenta que disponemos de 500 euros:

a) Cuando aumenta y cuando disminuye la rentabilidad

b) Cuanto dinero debemos invertir para obtener la máxima rentabilidad posible.

c) Cual será el valor de dicha rentabilidad.

Solución

a) La derivada primera nos da el crecimiento o decrecimiento de la función. Si la derivada es positiva la función crece y si es negativa decrece

Procedimiento:

-Se deriva la función:

R`(x)=-0,004x+0,8

-Se iguala a 0 y se resuelve la ecuación que resulta:

R`(x)=0 , 

 

-Se estudia el signo de la derivada a la derecha e izquierda de los valores que nos ha dado 0 la derivada (en este caso x =200). Hay varios métodos, uno muy mecánico:

 

se coge un punto menor que 200, por ejemplo 100, y sustituimos R´(100)=0,4>0 y en otro mayor que 200 (por ejemplo 300) R´(300)=-0,4<0

Entonces la derivada es positiva en el intervalo (0, 200), y f es creciente en ese intervalo y es decreciente en (200, 500) ya que en ese intervalo nos ha dado negativa la derivada. Lo que nos dice también que en punto 200 hay un máximo local

b) Teniendo en cuenta el apartado a debemos invertir 200 euros.

c) La máxima rentabilidad es R(200)= -0,002.(200)²+0,8.200-5=75 euros

 
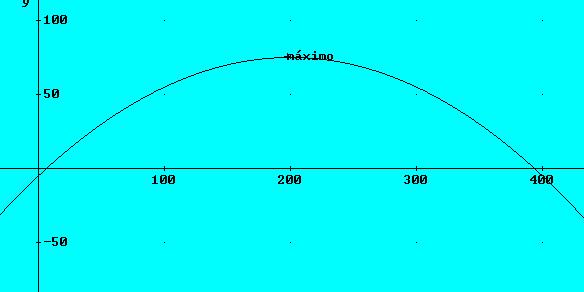
En la arquitectura se puede utilizar las derivadas para determinar un numero máximo o un numero mínimo de que es lo que utilicen dentro de una obra o bien para identificar el presupuesto para alguna inversión de material nuevo.

 BIBLIOGRAFIA

http://centros5.pntic.mec.es/ies.de.melilla/Extremos_relativos.htm
http://www.vitutor.com/fun/5/c_9.html
http://carmesimatematic.webcindario.com/optimacion.htm
http://www.sc.ehu.es/sbweb/fisica/cinematica/rectilineo/rectilineo.htm
http://www.matematicasfisicaquimica.com/matematicas-bachillerato/39-matematicas-bachillerato/659-ejercicios-solucion-calculo-derivadas-matematicas-bachillerato.html